Computational Teaching and Learning in Mathematics at UBC

Computational Teaching and Learning in Mathematics at UBC#

Patrick Walls

May 23, 2025

Land Acknowledgement#

BIRS in Banff is located on Treaty 7 territory, the traditional lands of the Stoney Nakoda Nations: the Goodstoney, Chiniki, and Bearspaw First Nations; three Nations of the Blackfoot Confederacy: the Piikani, Kainai and Siksika First Nations; the Tsuut’ina First Nation; and the Métis Nation of Alberta.

Mission, Goals and Principles#

Mission Statement#

For students to learn transferable knowledge and skills in computational thinking for mathematics.

Workshop Goals#

  • Outline a set of standards for computational teaching and learning in mathematics

  • Provide explicit software training for instructors

  • Create and share computational learning materials

Guiding Principles#

  • Mathematics before computing

  • Design for scale

  • Language agnostic

  • Align with open source community

  • Exploit institutional inertia

  • Keep it simple

Mathematical Computing at UBC#

Challenges#

  • Scale: How do we design curriculum to serve hundreds or thousands of students?

  • Student prior knowledge: How do we design curriculum for students with no prior knowledge of mathematical software and computing?

  • Instructor prior knowledge: How do we design curriculum for instructors with no prior knowledge of mathematical software and computing?

  • Limited resources: How do we design new curriculum using only the resources that we already have?

  • Sustainability: How do we design curriculum that will last?

Courses#

Courses where mathematical computing is integral to the learning objectives:

  • MATH 210 Introduction to Mathematical Computing

  • MATH 360 Introduction to Mathematical Modelling

  • MATH 441 Projects in Mathematical Optimization

  • MATH 461 Projects in Mathematical Modelling

Courses where mathematical computing is complementary to the learning objectives:

  • MATH 152 Linear Systems

  • MATH 215 Elementary Differential Equations I

  • MATH 221 Matrix Algebra

  • MATH 223 Linear Algebra

  • MATH 256 Differential Equations

  • MATH 302 Introduction to Probability

  • MATH 307 Applied Linear Algebra

  • MATH 316 Elementary Differential Equations II

See UBC Math Course Map for more info.

Software Stack#

  • Python is an open source general purpose programming language

  • Jupyter is a web-based development environment for creating computational documents

  • Syzygy is a collection JupyterHubs integrated with institutional authentication systems

  • NumPy is a Python package for numerical computation with arrays

  • SciPy is a Python library of algorithms for mathematical computing

  • Matplotlib is a Python package for mathematical graphics and data visualization

  • GitHub is a web-based platform for collaborating on software projects

  • nbgrader is a Python package for creating, autograding and managing assignments in Jupyter notebooks

  • CanvasAPI is a Python package for uploading/downloading data from Canvas

  • Jupyter Book is a Python package which creates web-based books from computational documents

Implementation#

  • Design computational learning materials with Python and Jupyter

  • Publish web-based learning material with Jupyter Book and GitHub

  • Collaborate with instructors to setup Canvas courses and assignments

  • Python TA training

  • nbgrader training for staff/TAs

  • Online Zoom lectures and co-teaching

  • Autograding with nbgrader and CanvasAPI

  • Supervise TAs and staff

  • Python TAs in Math Learning Center (MLC)

Examples#

Clone the repo: https://github.com/patrickwalls/examples.git

MATH 210 Introduction to Mathematical Computing#

  • Numerical integration, numerical methods for ordinary differential equations, eigenvalues and eigenvectors

  • 100 students 2 sections

  • Prerequisites: Calculus II, Linear Algebra, Differential Equations I

  • Live coding in class

  • Assignments autograded with nbgrader

  • Exams on paper including reading and writing Python code

  • Mathematical Python

MATH 152 Linear Systems#

  • Linear equations, vector geometry, linear transformations, eigenvalues and eigenvectors

  • 1000 students 5 sections

  • Bi-Weekly MATLAB computer labs on Zoom directed by MATLAB TAs

  • MATLAB assignments semi-autograded with mbgrader

  • No prior knowledge of MATLAB

  • Students use MATLAB Online

  • MATLAB for UBC Math

MATH 215 Elementary Differential Equations I#

  • First order equations, second order equations with constant coefficients, Laplace transform, linear systems, 2D nonlinear systems and linearization

  • 400 students 3 sections

  • Prerequisites: Calculus II, Linear Algebra I

  • No prior knowledge of Python and Jupyter

  • Python for UBC Math

MATH 307 Applied Linear Algebra#

  • Matrix decompositions LU, QR, SVD and discrete Fourier transform

  • 300 students 3 sections

  • Prerequisites: Calculus III and Linear Algebra I

  • No prior knowledge of Python and Jupyter

  • MATH 307 Notes

MATH 360 Introduction to Mathematical Modelling#

  • 80 students 1 section

  • Flipped classroom

  • Prerequisites: Mathematical Computing and Differential Equations I

  • Builds on Python and Jupyter knowledge and skills from MATH 210

  • MATH 360 Notes

MATH 441 Projects in Mathematical Optimization#

  • 40 students 1 section

  • Linear programming, combinatorial optimization, convex optimization

  • Project based with lecture time for collaborative group work

  • Prerequisites: Linear Prgramming

  • Assumes no prior knowledge of Python and Jupyter (but almost all students have MATH 210)

Simulate Student Experience#

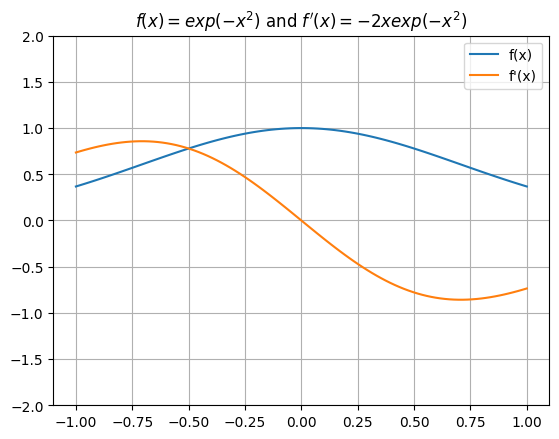
Plot the function \(f(x) = e^{-x^2}\) and its derivative \(f'(x)\) on \([-1,1]\).

How do the values of \(f'(x)\) correspond to the shape of the graph \(y = f(x)\)?

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-1,1,100)

f = lambda x: np.exp(-x**2)
df = lambda x: -2*x*np.exp(-x**2)

plt.plot(x,f(x))
plt.plot(x,df(x))
plt.grid(True)
plt.title("$f(x) = exp(-x^2)$ and $f'(x) = -2xexp(-x^2)$")
plt.legend(["f(x)","f'(x)"])
plt.ylim([-2,2])
plt.show()
../_images/16033b32657037a3998a9c290b650807220655a7e989d67771d5cfdbd94bb210.png

Thanks!

Contents